概要
↓こういう感じの離散なラベル列を視覚的にわかりやすくプロットしたいという話.
[2, 1, 1, 1, 0, 0, 1, 1, 2, 1, 1, 0, 0, 2, 2, 0, 0, 0, 1, 1]
カテゴリ系列のトイデータの生成
何を使ってもよいが,ここでは隠れマルコフモデルを実装したパッケージであるhmmlearnを用いてトイデータを生成した.隠れマルコフモデルといっても今回は離散状態のみを使っているため,実質的にはただのマルコフモデルである.
https://hmmlearn.readthedocs.io/en/latest/tutorial.html
ここでは,結果を再現できるように乱数のシードを固定している(np.random.seed(42)).
import numpy as np
from hmmlearn import hmm
np.random.seed(42)
model = hmm.GaussianHMM(n_components=3, covariance_type="full")
model.startprob_ = np.array([0.6, 0.3, 0.1])
model.transmat_ = np.array([[0.7, 0.2, 0.1],
[0.3, 0.5, 0.2],
[0.3, 0.3, 0.4]])
model.means_ = np.array([[0.0, 0.0], [3.0, -3.0], [5.0, 10.0]])
model.covars_ = np.tile(np.identity(2), (3, 1, 1))
X, Z = model.sample(100)
X2, Z2 = model.sample(100)
離散状態変数ZとZ2の中身を出力してみると以下のようになってるのがわかる.
Z2は複数の結果を同時にプロットする例で使う.
In [4]: Z
Out[4]:
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 1, 0, 0, 0, 0, 1, 0, 1, 2, 0,
1, 1, 1, 1, 0, 0, 0, 0, 2, 2, 2, 2, 0, 1, 1, 1, 1, 2, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 1, 2, 1, 2, 2, 0, 0, 0, 1, 1, 1, 1,
2, 2, 1, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 1, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
In [5]: Z2
Out[5]:
array([0, 1, 0, 0, 0, 0, 2, 1, 0, 1, 0, 1, 1, 2, 2, 2, 1, 0, 2, 1, 1, 1,
0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 2, 2, 2, 1, 1, 1, 0, 0, 0,
2, 2, 2, 1, 0, 2, 2, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 0, 0, 2, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 2, 2, 0, 2, 0, 0, 0, 0, 0])
カテゴリ系列のプロット
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
# cmap = plt.get_cmap('Pastel1')
cmap = ListedColormap(
np.array([(255, 75, 0),
(3, 175, 122),
(0, 90, 255)]) / 255
)
fig = plt.figure(figsize=(16, 4))
plt.imshow(
Z[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
plt.yticks([])
plt.show()
vmin=0 および vmax=2 はカテゴリ番号の最小値と最大値を明示的に指定している.
この例ではこれらのオプションが無くても出力結果は変わらないが,
Zの中に全てのクラスが出てきてないとき(例えば,0と2しかないとき),
Colormapからの色の選ばれ方が変わってしまうのでそれを防ぐためにいれてある
(複数の分類結果を比較したいときに影響してくる).
aspect='auto'が無いと高さ1ピクセルの平べったい画像が出力されてしまう.
また,interpolation='none'が無いと
カテゴリの変化の境目で画像のアンチエイリアスが誤ってかかってしまい,
実際のカテゴリと異なる出力結果になってしまうので注意
(実際に存在しないカテゴリが現れているように見える).
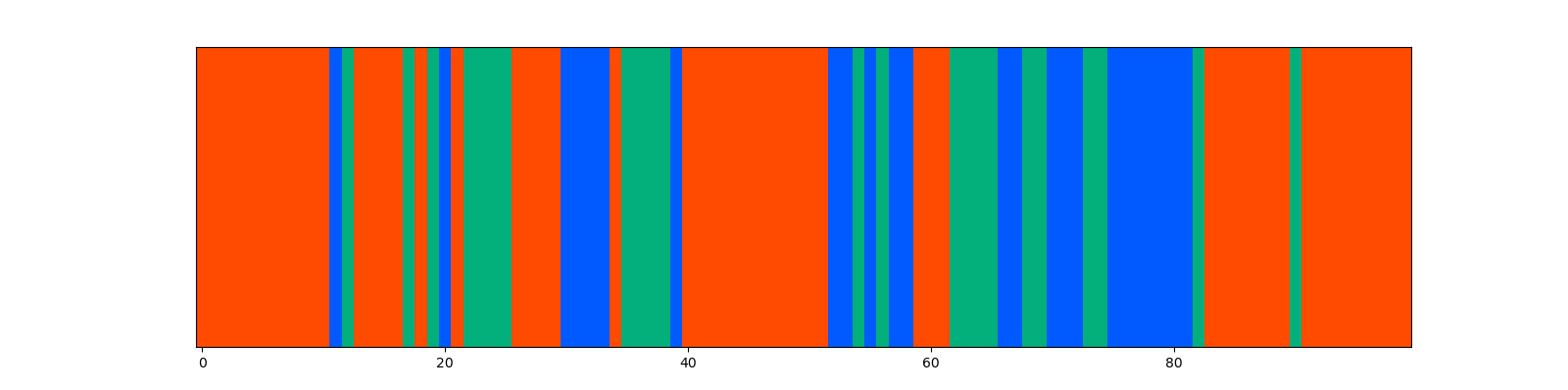
結果:
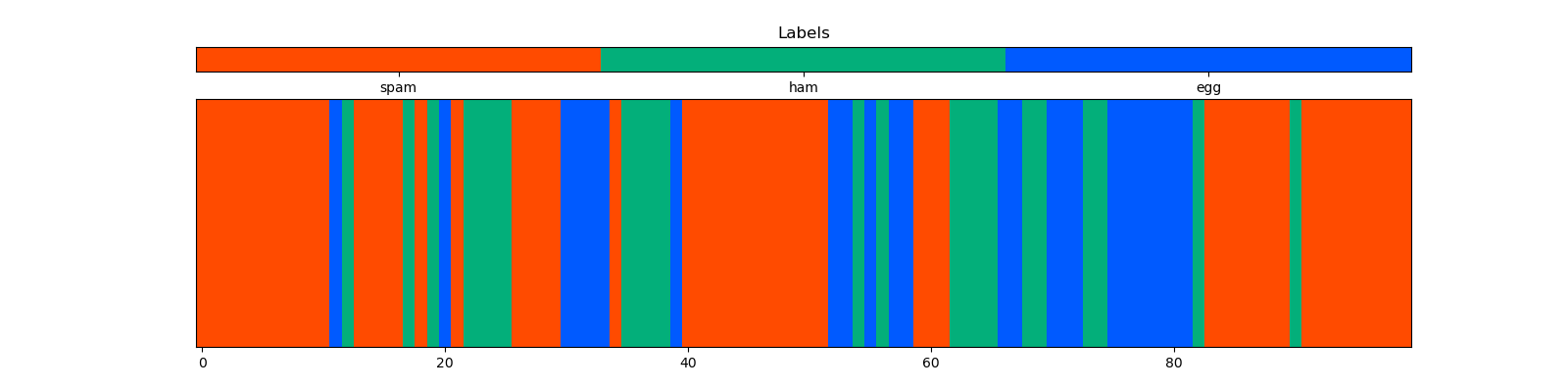
凡例付きのプロット
先ほどの例に出力の色がどのカテゴリに対応しているかを示す凡例を追加する.
これはMatplotlibのlegendsの機能を使わずに
Axisをひとつ追加して全ての色を含む配列をimshowをすることで対応する.
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
# cmap = plt.get_cmap('Pastel1')
cmap = ListedColormap(
np.array([(255, 75, 0),
(3, 175, 122),
(0, 90, 255)]) / 255
)
fig = plt.figure(figsize=(16, 4))
gs = plt.GridSpec(nrows=2, ncols=1, height_ratios=[0.1, 1])
ax = [fig.add_subplot(g) for g in gs]
labels = np.arange(3)
ax[0].imshow(
labels[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
ax[0].set_title('Labels')
ax[0].set_yticks([])
ax[0].set_xticks(labels)
ax[0].set_xticklabels(['spam', 'ham', 'egg'])
ax[1].imshow(
Z[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
ax[1].set_yticks([])
plt.show()
結果:
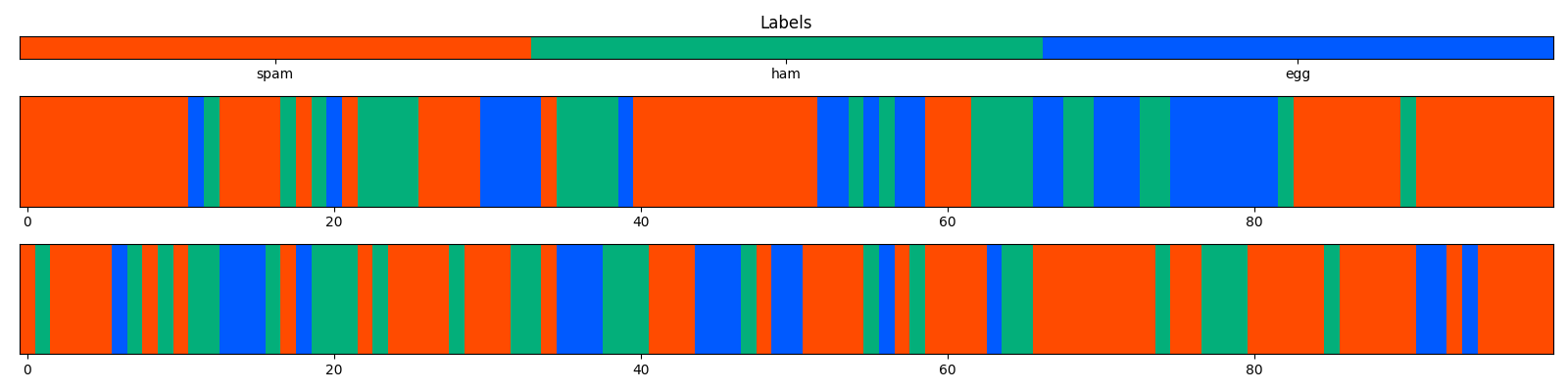
複数のカテゴリ系列を並べてプロット
上記の例にAxisを追加し,さらにX軸を共有する設定を行う.
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
# cmap = plt.get_cmap('Pastel1')
cmap = ListedColormap(
np.array([(255, 75, 0),
(3, 175, 122),
(0, 90, 255)]) / 255
)
fig = plt.figure(figsize=(16, 4))
gs = plt.GridSpec(nrows=3, ncols=1, height_ratios=[0.1, 0.5, 0.5]) # 3つ(ラベル用+結果2つ)
ax = [fig.add_subplot(g) for g in gs]
ax[2].sharex(ax[1]) # 2つの結果のx軸を共有する
labels = np.arange(3)
ax[0].imshow(
labels[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
ax[0].set_title('Labels')
ax[0].set_yticks([])
ax[0].set_xticks(labels)
ax[0].set_xticklabels(['spam', 'ham', 'egg'])
ax[1].imshow(
Z[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
ax[1].set_yticks([])
# 2つ目の結果
ax[2].imshow(
Z2[np.newaxis, :], cmap=cmap, vmin=0, vmax=2,
aspect='auto', interpolation='none'
)
ax[2].set_yticks([])
plt.tight_layout() # 見た目をきれいにする
plt.show()
結果:
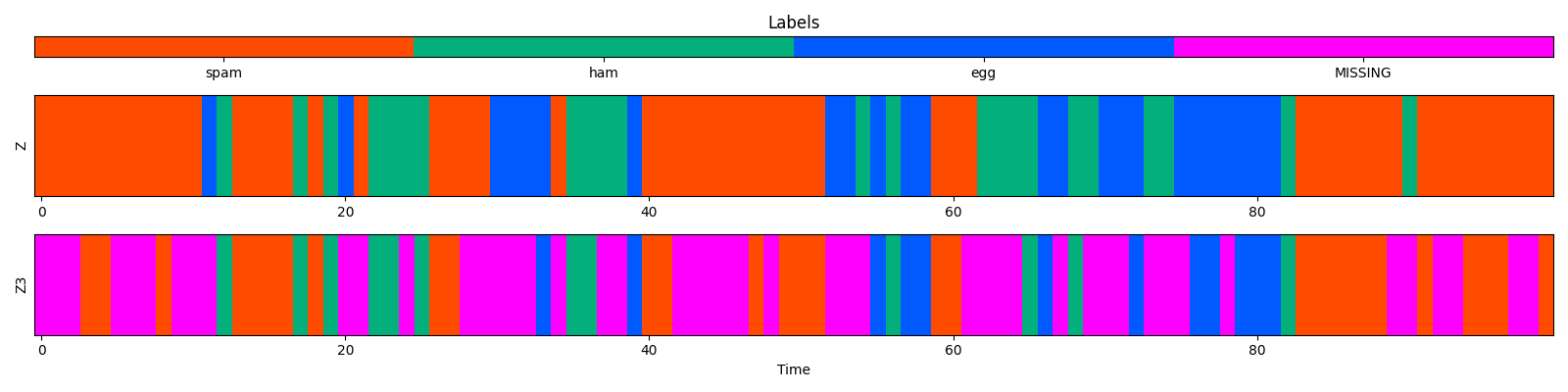
カテゴリに欠損値があるケース
欠損値を扱うためのデータ構造
まず,欠損値を扱うための配列である,numpy.ma.masked_arrayについて簡単に述べる.詳細は公式のリファレンスを参照されたい.
masked_arrayは通常のndarrayと使い方は同じだが,数値等のデータ配列に加えて同じサイズのmask配列を保持する.maskがTrueになっている成分は欠損しているとみなされる.
In [9]: a = np.arange(10)
In [10]: a_masked = np.ma.masked_array(a, mask=[0, 0, 0, 1, 0, 0, 1, 1, 0, 1])
In [11]: a_masked
Out[11]:
masked_array(data=[0, 1, 2, --, 4, 5, --, --, 8, --],
mask=[False, False, False, True, False, False, True, True,
False, True],
fill_value=999999)
# 普通の平均値
In [12]: a.mean()
Out[12]: 4.5
# 欠損値を無視した平均値
In [13]: a_masked.mean()
Out[13]: 3.3333333333333335
欠損をNaNや負の値として扱う方法もあるが,masked_arrayを使った方が欠損していない値との区別がしやすくなる.
欠損値を含むデータのプロット
まず,欠損値のあるデータZ3を適当に作っておく.
In [14]: mask = np.random.randint(2, size=100)
In [15]: mask
Out[15]:
array([1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0,
0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0])
# Zにマスクを被せる
In [16]: Z3 = np.ma.masked_array(Z, mask=mask)
欠損値を含むデータのプロットは以下の通り.
カラーマップにset_badで欠損値の色を指定しラベルも欠損値込みの配列に変えれば,あとは軸名とか調整するだけ.
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
# cmap = plt.get_cmap('Pastel1')
cmap = ListedColormap(
np.array([(255, 75, 0),
(3, 175, 122),
(0, 90, 255)]) / 255
)
cmap.set_bad(color='magenta') # 欠損値に対応する色を設定する
fig = plt.figure(figsize=(16, 4))
gs = plt.GridSpec(nrows=3, ncols=1, height_ratios=[0.1, 0.5, 0.5]) # 3つ(ラベル用+結果2つ)
ax = [fig.add_subplot(g) for g in gs]
ax[2].sharex(ax[1]) # 2つの結果のx軸を共有する
labels = np.ma.masked_array([[0, 1, 2, 3]], mask=[0, 0, 0, 1])
ax[0].imshow(labels, aspect='auto', cmap=cmap)
ax[0].set_title('Labels')
ax[0].set_yticks([])
ax[0].set_xticks([0, 1, 2, 3])
ax[0].set_xticklabels(['spam', 'ham', 'egg', 'MISSING'])
ax[1].imshow(Z[np.newaxis, :], aspect='auto', cmap=cmap, interpolation='none', vmin=0, vmax=2)
ax[1].set_yticks([])
ax[1].set_ylabel('Z')
ax[2].imshow(Z3[np.newaxis, :], aspect='auto', cmap=cmap, interpolation='none', vmin=0, vmax=2)
ax[2].set_yticks([])
ax[2].set_xlabel('Time')
ax[2].set_ylabel('Z3')
plt.tight_layout()
plt.show()
結果: